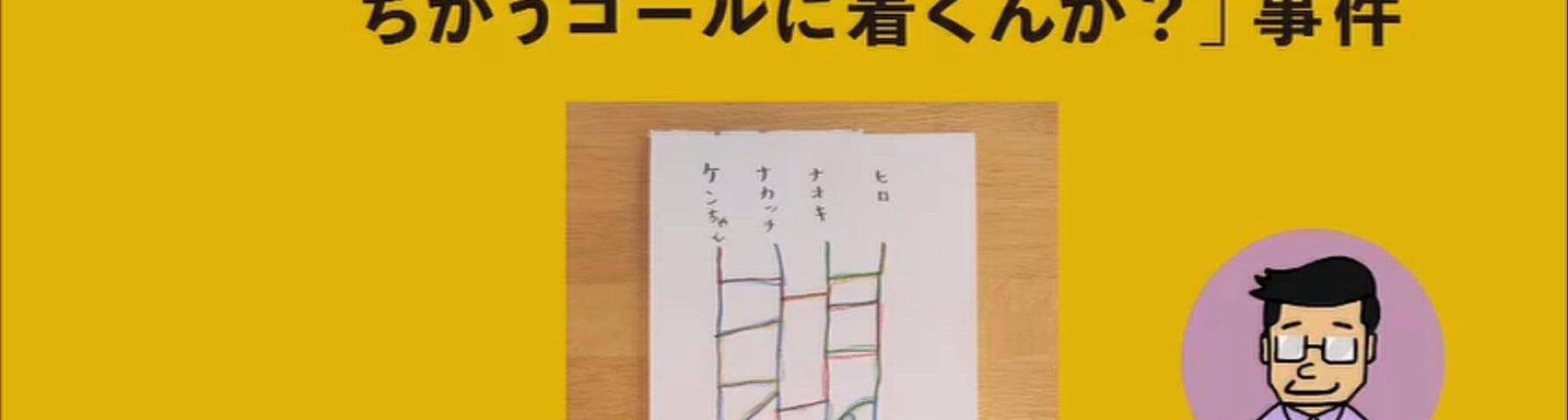
そういえば今日の0655では以下の写真の問題が出ました。
これは言い換えるとあみだくじの上の個数と下の個数は必ず同じであると証明可能なのか? という話です。
あみだくじにおいて「横線を引く」という行為は実は交換規則を追加するという行為になります。これは必ず 一対一 で入れ替え操作です。入れ替えなので総数に変化はありません。なので必ず同じです。
入れ替え操作について具体例を書くと
1 2 3 4
| | | |
a b c d
に対して
1 2 3 4
| | | – |
a b c d
と横線を引くことは
(1234)
↓
(abcd)
の対応を
(1234)
↓
(abdc)
とします、という話です。3->cを3->dにします、という感じ。個数に変更はありませんね。
ちなみにこれは大学数学では群論というのがあり、それの入り口で必ずやるやつです。授業であみだくじの例が出るかはわからないですがみんな頭に浮かんでるはずです。
さらにさらに群論を使うと、この中に嘘つきがいてそれは誰でしょう、みたいな問題も機械的に解けるようになります。公務員試験にあるらしいやつです。配点に対して必要な努力が合わないのでそのためにやるにはお勧め出来ませんが笑
数学にいた時は群論の強さがわかってなかったですが、情報系だと結構使い道あるらしいので勉強し直さないとと思っている筆頭です。
ちなみに明日答え合わせなので私と同じ話が出るかはわからないです笑